Khi nghiên cứu về đường tròn, hầu hết chúng ta đều đã biết đến các khái niệm như bán kính, đường kính, tiếp tuyến, nhưng có một khái niệm khác cũng quan trọng không kém, đó chính là “cát tuyến”. Cát tuyến mang trong mình những đặc tính toán học thú vị và là cầu nối giữa các hình học cơ bản và ứng dụng thực tế. Bài viết này sẽ đưa ra cái nhìn tổng quan về cát tuyến và hướng dẫn cách vẽ chúng trong hình học đường tròn.
Cát Tuyến Của Đường Tròn Là Gì
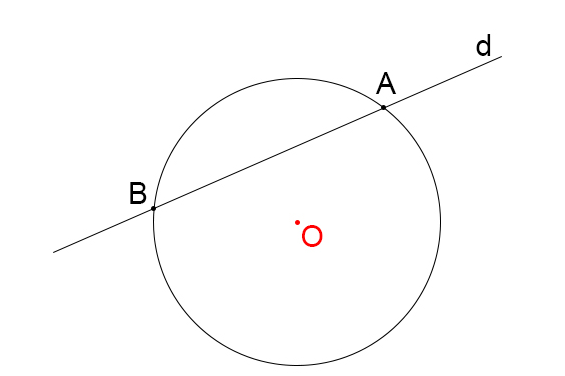
Cát tuyến của đường tròn là một đường thẳng cắt đường tròn tại hai điểm. Nếu so sánh với tiếp tuyến – đường thẳng chỉ chạm vào đường tròn tại một điểm duy nhất – thì cát tuyến có thể được coi là “đối lập” vì nó thực sự cắt qua và mở ra đường tròn, tạo thành một phần của mặt cắt.
Cách Vẽ Cát Tuyến Của Đường Tròn
Vẽ một cát tuyến không quá phức tạp, nhưng cần thực hiện đúng các bước sau để đảm bảo tính chính xác:
- Vẽ một đường tròn với tâm O và bán kính r tùy ý.
- Chọn một điểm A bên trong hoặc ngoài đường tròn, nơi bạn muốn cát tuyến bắt đầu.
- Vẽ một đường thẳng qua A và cắt đường tròn tại hai điểm B và C. Đoạn thẳng BC chính là cát tuyến của đường tròn mà bạn vừa vẽ.
Cát Tuyến Trong Đường Tròn Là Gì
Cát tuyến trong đường tròn không chỉ đơn giản là định nghĩa trên mặt hình học mà nó còn xuất hiện trong nhiều bài toán thực tế. Trong một số trường hợp, cát tuyến còn liên quan đến việc tính toán độ dài dây cung hay xác định vị trí các điểm trên đường tròn thông qua các bài toán liên quan đến tính chất của góc và đoạn thẳng.
Tính Chất Cát Tuyến Đường Tròn
Một trong những tính chất quan trọng của cát tuyến là tích của khoảng cách từ một điểm nằm trên cát tuyến đến hai điểm cắt đường tròn là một hằng số. Nghĩa là, nếu ta lấy điểm A trên cát tuyến và đo khoảng cách từ A đến B và từ A đến C, thì AB*AC sẽ luôn giữ nguyên không đổi, bất kể vị trí của A trên cát tuyến (miễn là A không trùng với B hoặc C.
Cát tuyến của đường tròn là một cửa sổ mở ra không chỉ về mặt toán học mà còn trong cách chúng ta tiếp cận và giải quyết các vấn đề trong thế giới thực. Từ việc tìm hiểu khái niệm đến cách vẽ và sử dụng các tính chất của cát tuyến, chúng ta có thể nâng cao khả năng hiểu và áp dụng hình học vào cuộc sống, từ kiến trúc đến vật lý, từ nghệ thuật đến các lĩnh vực kỹ thuật. Vẽ và nghiên cứu cát tuyến là một phần của việc học toán, nhưng hiểu được chúng có nghĩa là mở rộng cánh cửa tri thức và sáng tạo của bản thân.