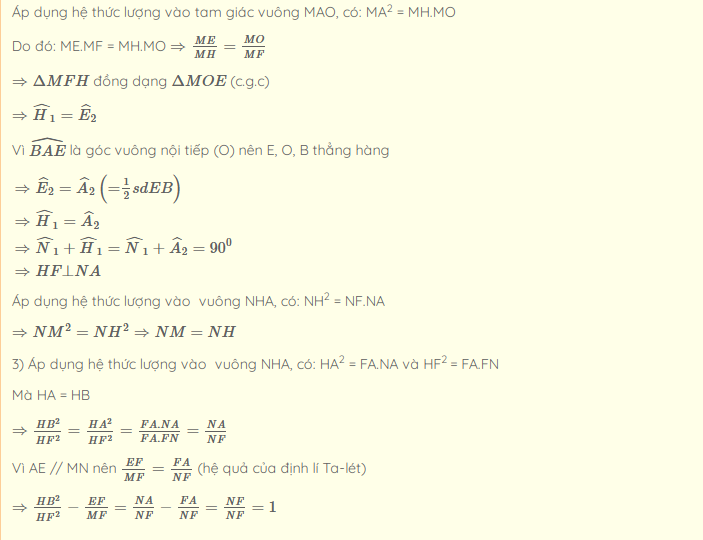Bài 1: Cho nửa đường tròn tâm O có đường kính AB = 2R. Kẻ hai tiếp tuyến Ax, By của nửa đường tròn (O) tại A và B (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng có bờ là đường thẳng AB). Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ tiếp tuyến với nửa đường tròn, cắt tia Ax và By theo thứ tự tại C và D.
a) Chứng minh tam giác COD vuông tại 0;
c) Kẻ MH vuông góc AB (H ∈ AB). Chứng minh rằng BC đi qua trung điểm của đoạn MH.
Bài 2: Cho nửa đường tròn (O), đường kính AB và một dây cung CD. Kẻ AE và BF vuông góc với CD lần lượt tại E và F. Chứng minh:
Bài 3: Cho đường tròn tâm O, bán kính R. Từ một điểm M ở ngoài đường tròn, kẻ hai tiếp tuyến MA và MB với đường tròn (A, B là các tiếp điểm). Qua A, kẻ đường thẳng song song với MO cắt đường tròn tại E (E khác A), đường thẳng ME cắt đường tròn tại F (F khác E), đường thẳng AF cắt MO tại N, H là giao điểm của MO và AB.
1) Chứng minh: Tứ giác MAOB nội tiếp đường tròn.
2) Chứng minh: MN2 = NF.NA vả MN = NH.
3) Chứng minh: (HB^2/HF^2) – EF/MF = 1
Bài 4: Trong mặt phẳng tọa độ Oxy cho đường tròn (C) có phương trình x^2 + y^2 + 2x -4y -4=0 .tìm ảnh của (C) qua phép tịnh tiến theo vecto v = (2;-3)